ME 528

ME 528

Numerical Heat Transfer

This course is the equivalent of a Computational Fluid Dynamics (CFD) course. After covering the fundamentals of numerical solution, three mainstream methods, namely Finite Difference, Finite Volume, and Finite Element are discussed.

Prerequisite(s): CS 108 and ME 421 or consent of instructor.

Office Hours                                                            Course Syllabus                                                    Course Scheduled

Not in session                                                                 Download                              This Course will next be offered ... 

Project 1
Time Developing Flow in a Parallel Plate Channel

We consider the time evolution of a flow in a parallel plate channel. The fluid is considered initially be at rest, and then evolves to its steady state solution.

The governing Navier-Stokes equations for this flow may be simplified to:

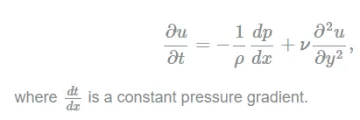
Navier-Stokes equation for this flow

For this project, the student is expected to:

  • State the boundary conditions for the problem
  • Non-dimensionalize the boundary conditions and governing equation
  • Mathematically determine the analytical solution
  • Write a numerical finite-difference code in either Fortran or C/C++ using:
    • An explicit method
    • An implicit method
    • 4th-order Runge-Kutta method
  • Investigate the following:
    • Accuracy considering the effects Δt, Δy, and r = Δt/(Δy)2
    • Stability considering the effects of Δt, Δy, and r
Sample Result

The video depicts the solution to this problem using an forward in time, central in space (FTCS), finite-difference scheme

 

Project Handout

The project handout may be downloaded here.

Project 2
Time Developing Flow in a Lid Driven Cavity


In this project, the student will develop a two-dimensional incompressible Navier-Stokes solver. The numerical method is based on the Marker and Cell approach by Harlow and Welch.

The code will then be used to solve a benchmark problem, the lid driven cavity, in order to verify its accuracy.

For this project, the student is expected to:

  • State the boundary conditions for the problem
  • Non-dimensionalize the boundary conditions and governing equations
  • Write an explicit MAC method code in either Fortran or C/C++
  • Compare with previously published results for the one-sided lid-driven cavity
  • Investigate:
    • The effect of Reynolds number
    • Stability considering the effects of Δt and Δx = Δy
Sample Result

Here we see an example of the flow in a single-lid driven cavity at Reynolds number equal to 100. The solution is shown with velocity vectors and vorticity. Note that the solution is laminar and steady.

Benchmark Data

Validation data may be downloaded here:
Benchmark Validation Data [PDF]

Sample Result

Here we see an example of the flow in a single-lid driven cavity at Reynolds number equal to 10,000. Note that the velocity vectors are not steady, and a quasi-steady behavior emerges.

Project Handout

The project handout may be downloaded here