ME 594

ME 594

Computational Compressible Flow

This course is focused primarily on supersonic flows. It covers fundamental mathematical descriptions of benchmark linear and nonlinear problems, leading to the numerical solution of the Riemann Problem for Euler equations.

Prerequisite(s): CS 108 and ME 428 or consent of instructor.

Office Hours                                                   Course Syllabus                                              Course Schedule
                 TBD                                   The course syllabus is available for download               Fall 20xx; Day and time TBD

Project 1
Exact Solution of the Riemann Problem for Euler Equations in 1D

This project deals with the exact solution of the Riemann Problem for 1D Euler equations, as discussed in Chapter 4 of Toro’s book. Start from the source code E1RPEX.F in the library NUMERICA that is available online.

For this project, the student is expected to:

  • Run the code for tests 1 through 5
  • Modify the subroutine GUESSP to enforce the coice of initial guess values
  • Modify the boundary conditions for tests 1 through 5 and compare to the initial case
Sample Result

Exact solution for density, velocity, pressure and specific internal energy for ρL = 1.0 at t = 0.15 units and for ρL = 0.2 at t = 0.1 units.

density velocity pressure

Project Handout

The project handout may be downloaded here

Project 2

Godunov Method for 1D Inviscid Burgers Equation

This project deals with the solution of the 1D inviscid Burgers equation using the Godunov method described in Chapter 5 of Toro’s book. Start from the source code BUGOD.F in the library NUMERICA that is available online.

For this project, the student is expected to:

  • Run the code for Test 3 in Chapter 5 to validate the code
  • Modify subroutine BCONDI to implement Dirichlet type boundary conditions
  • Obtain numerical results for the 1D Burgers equation with periodic boundary conditions
  • Determine the effect of Δt on stability
  • Determine the effect of Δx on numerical diffusion
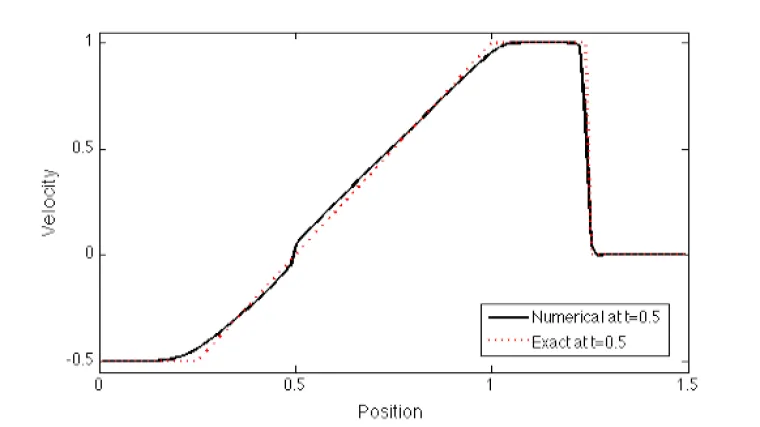
 Sample Result

Exact solution for velocity with transmissive boundary conditions.

transmissive boundary solution

Project Handout

The project handout may be downloaded here

Project 3
Godunov Method for 1D Euler Equations
 

This project deals with the solution of the 1D Euler equations using the Godunov method described in Chapter 6 of Toro’s book. Start from the source code E1GODS.F in the library NUMERICA that is available online.

For this project, the student is expected to:

  • Run the code for Tests 1 to 5 in Chapter 6 and validate the results
  • Run Tests 1 to 5 for REFLECTIVE boundary conditions and compare the results with the results from part 1
  • Study the effect of INTERCELL FLUX for Tests 1 to 5
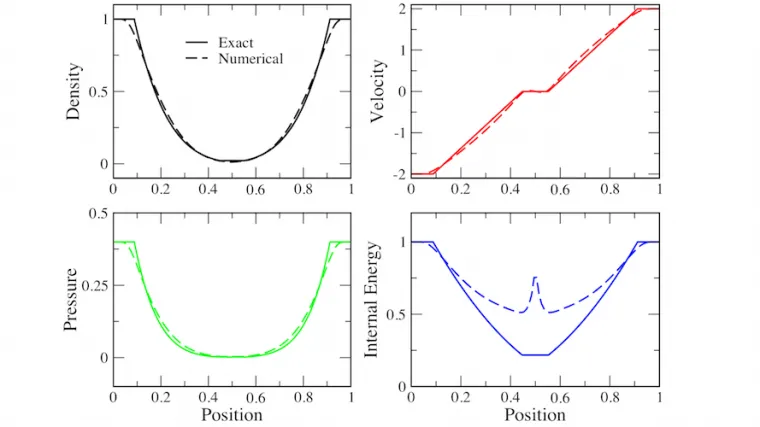
 Sample Result

Test 2 at t = 0.15 units.

sample result 594

 Project Handout

The project handout may be downloaded here